Phasenwinkel φ messen / berechnen

Für fast jedes Oszilloskop - auch für 1-Kanal-Oszilloskope

Im Folgenden werden drei einfache Möglichkeiten vorgestellt, wie man mithilfe eines Oszilloskops den Phasenwinkel - also den zeitlichen Versatz zweier Sinuskurven - einfach, schnell und relativ genau messen bzw. berechnen kann.

*Animation: Phasenverschiebung - oben als Oszillogramm, unten als Lissajous-Figur.*

Die Phasenverschiebung bzw. der Phasenwinkel ist für viele praktische Anwendungen von Bedeutung. Diese reichen vom einfachen Filter (z.B. Tiefpass) über Transistoren und Operationsverstärker bis hin zum Kraftstrom mit drei, jeweils um 120° versetzte Phasen.

Die Phasenverschiebung kann u.a. mit einer kleinen Schaltung bestehend aus einem Kondensator und einem Widerstand erzeugt werden.

*Bild: Phasenverschiebung mit einem Kondensator und einem Widerstand im fliegenden Aufbau auf dem Testboard.*

*Bild: Das zugehörige Oszillogramm zum Aufbau auf dem Testboard.*

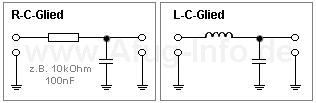Zum Testen und Üben der Berechnungsmethoden kann man die Phasenverschiebung natürlich ersatzweise auch mit einem Signalgenerator (oder einem kleinen Netztrafo/Klingeltrafo) erzeugen.

Methode 1

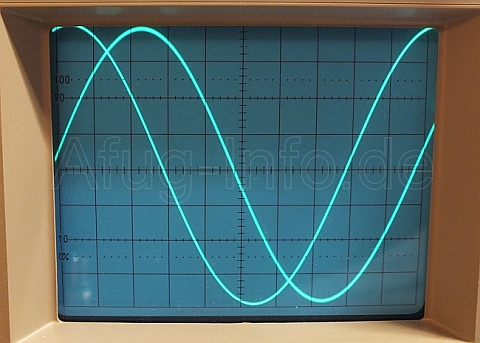
Benötigt wird ein 2-Kanal-Oszilloskop. Ein Signal wird über Kanal 1 und das andere über Kanal 2 eingespeist. Beide Sinus-Wellen sollten auf dem Bildschirm in etwa dieselbe Amplitude ("Höhe") in DIVs haben, einstellbar über die Volt/DIV-Regler des Oszis; mit den Positions-Reglern des Oszis lassen sich die Signale entsprechend positionieren.

*Bild: Eine mögliche Messanordnung könnte so aussehen.*

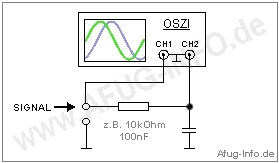Zunächst zählt man, wieviele horizontale DIVs ("Kästchen" auf der horizontalen Nulllinie des Oszilloskops) eine einzelne vollständige Periodendauer einer Sinuswelle beinhaltet. Das Ergebnis wird als Wert B in die nachstehende Formel eingesetzt.

Für ein bequemes Ablesen und ein möglichst genaues Ergebnis kann man die Zeitbasis des Oszilloskops so einstellen, dass eine Periodendauer über den gesamten Bildschirm reicht.

Anschließend zählt man die Anzahl der DIVs, die auf der horizontalen Null-Linie zwischen den beiden Sinuskurven liegen (Wert A), und teilt diesen Wert durch den vorher gezählten Wert B.

Das Ergebnis multipliziert man dann noch mit 360 und erhält den Phasenwinkel.

Als Formel ausgedrückt, ist es gleich viel übersichtlicher. Zusätzlich illustrieren nachfolgende Bilder den Vorgang anschaulich.

Beispiel: 5 : 20 * 360 = 90° Phasenwinkel

Wer die Bildschirmvergrößerungsfunktion des Oszis (falls vorhanden) nutzt, bitte nicht vergessen, den Vergrößerungsfaktor in die Berechnung miteinzubeziehen.

Eine Periodendauer entspricht 360 Grad. Wenn eine Periodendauer 10 DIVs einnimmt, dann entspricht in diesem Beispiel 1 DIV einem Zehntel von 360° bzw. einem Winkel von 36° (360° : 10 = 36°; Gegenrechnung: 10 * 36° = 360°).

Wenn die beiden Sinuswellen also um 2 DIVs gegeneinander verschoben sind, beträgt der Phasenwinkel 2 * 36° = 72°.

Wer es sich so leichter merken kann, kann die Formel natürlich auch umstellen: φ = 360 : B * A

Wenn Cursor zur Verfügung stehen, kann man die Periodendauer (Wert B) und die Differenz zwischen den Signalen (Wert A) auch damit vermessen. A und B sollten lediglich auf eine Einheit gebracht werden, z.B. beide in Sekunden oder in ms oder in µS, und können dann in die Formel A/B*360 eingesetzt werden.
z.B. 0,092mS / 1mS * 360 = 33,12°

Bild: 60 Grad Phasenwinkel als Beispiel. Beide Sinuskurven sollen in etwa dieselbe Höhe in DIVs haben. Der Wert B ergibt sich aus der Anzahl der horizontalen DIVs einer Periodendauer, gemessen auf der Null-Linie des Oszilloskops. Die Null-Linie ist mit einem grünen Pfeil am rechten Rand markiert. Hier sind es 10 Kästchen, der Wert B ist folglich 10.
Der Wert A entspricht der Anzahl der DIVs ("Kästchen") zwischen den beiden Sinuskurven (Versatz), wiederum gemessen an der horizontalen Null-Linie des Oszilloskops. Hier sind es 1,67 DIVs. Die Rechnung lautet demnach: 1,67 : 10 * 360 = 60 Grad.

*Bild: 120 Grad Phasenwinkel als Beispiel. A ist 3,35, der Wert B ist wiederum 10.*

Diese Art der Berechnung ist eine einfache Variante, bei der es nichts weiter zu beachten gibt.

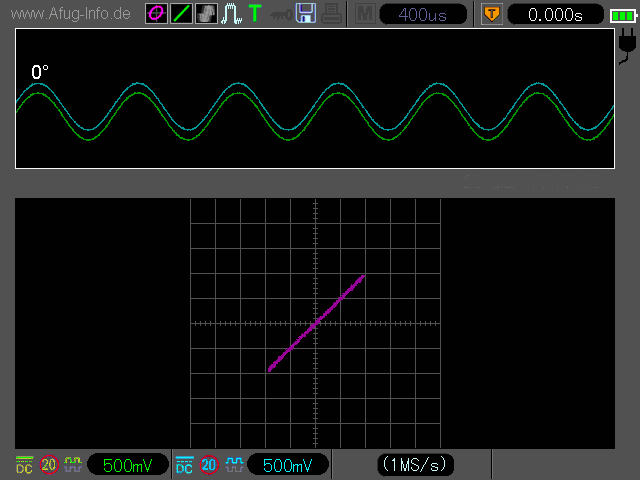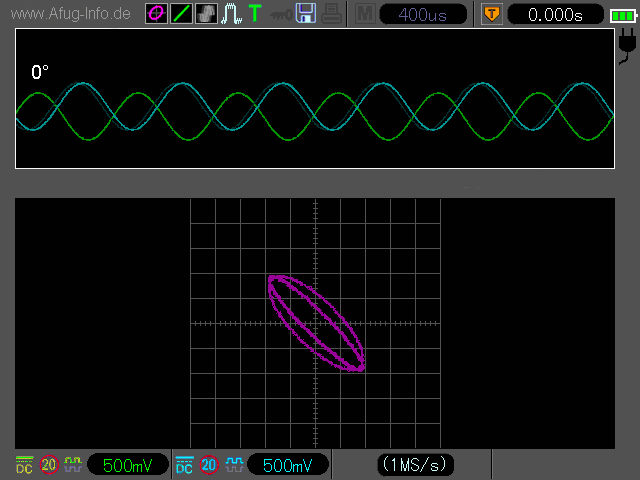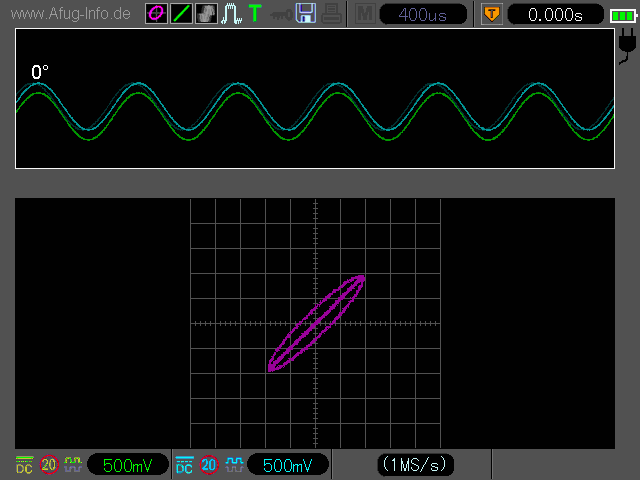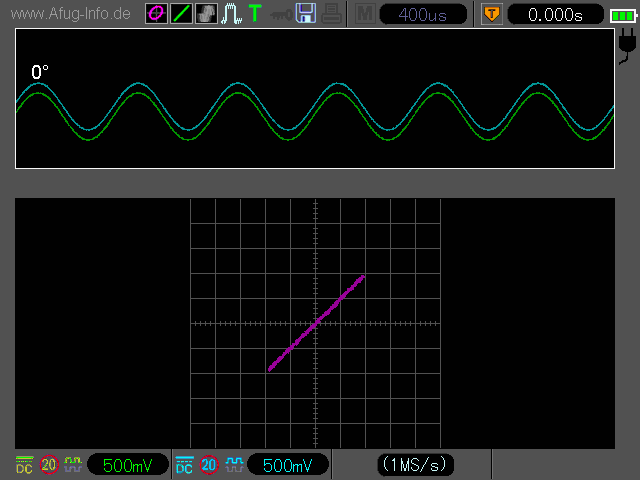
Den Phasenwinkel kann man auch mithilfe des XY-Betriebs ermitteln. Hierbei sind allerdings ein paar Besonderheiten zu berücksichtigen und ein Taschenrechner ist erforderlich.

Methode 2

Bei 2-Kanal-Oszilloskopen erfolgt der Anschluss wie oben bereits unter Methode 1 beschrieben. Den Oszi schaltet man dann in den X-Y-Betrieb.

Bei 1-Kanal-Oszilloskopen verwendet man den Kanal-Eingang und den X-Eingang. Das Oszilloskop schaltet man in den XY-Betrieb und positioniert den Punkt in die Mitte des Bildschirms. Dann legt man das erste Signal am Kanaleingang an, stellt die Signallänge ein und klemmt es wieder ab. Anschließend speist man das zweite Signal über den X-Eingang ein und stellt dieselbe Signallänge (DIVs) wie beim Kanaleingang ein. Erst danach speist man auch das erste Signal wieder ein, so dass beide Signale anliegen und eine Lissajous-Figur auf dem Bildschirm erscheint.

Hat man seinen 1- oder 2-Kanal-Oszi entsprechend eingestellt, zählt man anschließend die Anzahl der DIVs, die die Lissajous-Figur in ihrer Gesamthöhe einnimmt (Wert B).

Dann zählt man die Anzahl der DIVs zwischen der oberen und der unteren Schnittstelle der Lissajous-Figur mit der vertikalen Mittellinie des Oszilloskops (Wert A).

Nun teilt man A durch B und nimmt von diesem Ergebnis den arcsin bzw. sin-1 (Schreibweise ist von Taschenrechner zu Taschenrechner unterschiedlich, die Funktion ist aber identisch).

Bei dieser Methode ist zu beachten, dass der arcsin nur bis 90° berechnet werden kann. Für alle größeren Phasenwinkel muss die Formel entsprechend modizifiert werden. Für Winkel von 90 bis 180 Grad wird das Rechenergebnis zusätzlich noch von 180 subtrahiert. Für Winkel von 180 bis 270 addiert man das errechnete Ergebnis zu 180 hinzu und für Winkel von 270 bis 360 zieht man das Rechenergebnis von 360 ab.

Beispiel: arcsin (5 : 10) = 30°

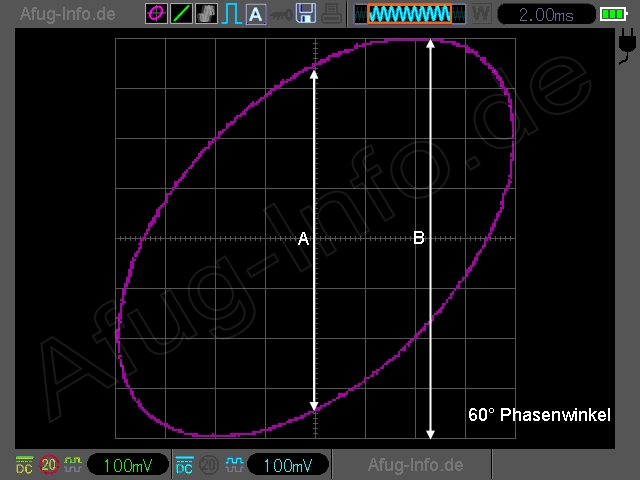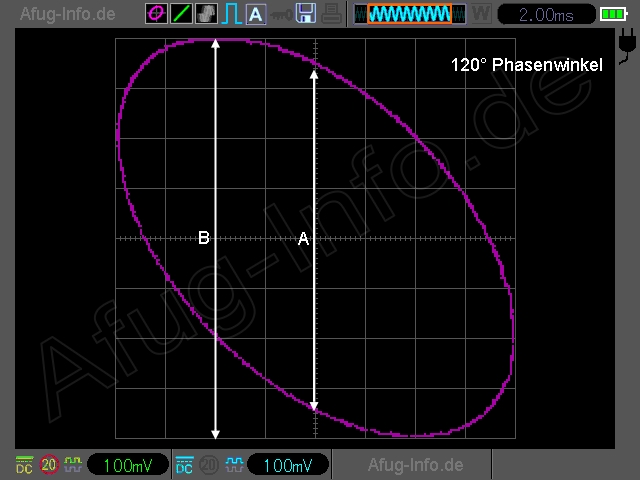Man sollte also schon vor der Berechnung grob wissen, in welchen Größenbereich der Phasenwinkel fällt. Das kann man in den meisten Fällen der Position der Lissajous-Figuar auf dem Oszi-Bildschirm entnehmen, jedoch nicht in allen. Der aufmerksame Beobachter wird bemerkt haben, dass die Lissajous-Figur bei manchen Phasenwinkeln identisch aussieht, z.B. bei 90° und 270° (jeweils ein Kreis) - siehe Animation oben. Das erfordert ggfs. eine zusätzliche Berechnung nach der ersten Methode.

Die zweite Berechnungsvariante ist damit nicht ganz so komfortabel wie die erste.

Methode 3 - für 1-Kanal-Oszilloskope

Bei der dritten Methoden sind 1 Kanal und der externe Trigger-Eingang ausreichend. Zuerst verbindet man der erste Signal mit dem Eingangskanal des Oszilloskops und triggert es intern, wobei man sich die Position des Signals am Triggerpunkt merkt. Dann verbindet man das zweite Signal mit dem externen Trigger-Eingang und triggert das erste Signal extern. Dann vergleicht man, wieweit sich das Signal vom Triggerpunkt (interner Trigger) entfernt hat. Diese Differenz ist der Wert A. Der Wert B ist wieder eine ganze Periodendauer. Der Rechenweg ist identisch wie oben bei der ersten Methode beschrieben: Phasenwinkel = A / B * 360

Fazit

Insbesondere die hier vorgestellte erste und dritte Berechnungsvariante sind einfach und mithilfe der Grundrechenarten durchzuführen und die dritte Variante funktioniert selbst mit älteren 1-Kanal-Oszilloskopen. Die zweite Methode erfordert mehr Aufmerksamkeit sowie einen Taschenrechner, führt aber ebenso zu Ergebnissen. Egal, welche Methode, die Genauigkeit des Ergebnisses ist davon abhängig, wie genau die Werte vom Oszi-Bildschirm abgelesen werden. Bei Ablese-Ungenauigkeiten kann es vorkommen, dass der berechnete Wert 117° ergibt, der Phasenwinkel tatsächlich aber 120° beträgt. Im Gesamtergebnis liefern die Methoden aber relativ genaue Ergebnisse, mit denen es sich arbeiten lässt.

Alle Inhalte sind urheberrechtlich geschützt. Jegliche Nutzung/Vervielfältigung bedarf der vorherigen schriftlichen Genehmigung. Copyright: www.Afug-Info.de Kontakt: http://www.afug-info.de/

Seitenanfang